Simple forward model#
Now we have some crystallographic functions and we can handle the detector geometry, we can perform a basic forward model of a single crystal to reassure ourselves that this wasn’t all for nothing!
[1]:
import jax
jax.config.update("jax_enable_x64", True)
import jax.numpy as jnp
from jax.scipy.spatial.transform import Rotation as jR
from matplotlib import pyplot as plt
import anri
import time
start = time.time()
In
Anri, all fundamental functions and transforms are written for single vectors.This was written to significantly simplify the functions themselves, keeping them easy to understand.
Additonally, when forward simulating many grains or voxels, you will likely have more complicated array shapes, so it makes sense to leave the broadcasting to the user or another part of the program for now.
I’m currently still grappling with the best way to expose vmapped functions in the API, so for now I will manually declare them here:
[2]:
# easy example: many hkls, single B matrix, so we vmap over hkls only, giving us [0, None]
omega_solns_vec = jax.vmap(anri.diffract.omega_solns, in_axes=[0, None, None])
sample_to_lab_vec = jax.vmap(anri.geom.sample_to_lab, in_axes=[0, 0, None, None, None, None])
q_lab_to_k_out_vec = jax.vmap(anri.diffract.q_lab_to_k_out, in_axes=[0, None])
raytrace_to_det_vec = jax.vmap(anri.geom.raytrace_to_det, in_axes=[0, None, None, None, None])
q_lab_to_tth_eta_vec = jax.vmap(anri.diffract.q_lab_to_tth_eta, in_axes=[0, None])
Crystallography#
Let’s take a simple Fe CIF file
[3]:
struc = anri.crystal.Structure.from_cif("../../../tests/data/cif/Fe.cif")
We generate some hkls:
[4]:
dsmax = 2.0
wavelength = 0.3
struc.make_hkls(dsmax=dsmax, wavelength=wavelength)
[5]:
struc.rings_dict[0]
[5]:
shape: (12, 7)
| h | k | l | tth | ds | intensity | ring_id |
|---|---|---|---|---|---|---|
| i64 | i64 | i64 | f64 | f64 | f64 | u32 |
| 0 | -1 | 1 | 8.498266 | 0.493956 | 1363.448082 | 0 |
| 1 | 1 | 0 | 8.498266 | 0.493956 | 1363.448082 | 0 |
| -1 | 0 | 1 | 8.498266 | 0.493956 | 1363.448082 | 0 |
| -1 | 0 | -1 | 8.498266 | 0.493956 | 1363.448082 | 0 |
| -1 | -1 | 0 | 8.498266 | 0.493956 | 1363.448082 | 0 |
| … | … | … | … | … | … | … |
| 1 | -1 | 0 | 8.498266 | 0.493956 | 1363.448082 | 0 |
| 0 | -1 | -1 | 8.498266 | 0.493956 | 1363.448082 | 0 |
| 0 | 1 | -1 | 8.498266 | 0.493956 | 1363.448082 | 0 |
| 0 | 1 | 1 | 8.498266 | 0.493956 | 1363.448082 | 0 |
| -1 | 1 | 0 | 8.498266 | 0.493956 | 1363.448082 | 0 |
Let’s generate a random orientation.
[6]:
key = jax.random.key(time.time_ns())
random_euler = jax.random.uniform(key, shape=(3,), minval=-90.0, maxval=90.0)
U = jR.from_euler('XYZ', random_euler, degrees=True).as_matrix()
U
[6]:
Array([[ 0.60321755, 0.50523376, 0.61714458],
[-0.53804769, -0.31340961, 0.78248265],
[ 0.5887557 , -0.80406048, 0.08278568]], dtype=float64)
Now we can generate some scattering vectors in the sample frame:
[7]:
UB = U @ struc.B
q_sample = (UB @ struc.ringhkls_arr.T).T
q_sample.shape
[7]:
(380, 3)
Ewald condition#
Now we can determine the omega angles required to diffract:
[8]:
chi = 0.0
wedge = 0.0
dty = 0.0
y0 = 0.0
# define incoming wavevector in the lab frame
k_in_lab = jnp.array([1., 0, 0])
k_in_lab_norm = anri.diffract.scale_norm_k(k_in_lab, wavelength)
# map it into the sample frame
k_in_sample_norm = anri.geom.lab_to_sample(k_in_lab_norm, 0.0, wedge, chi, dty, y0)
# etasign +1:
omega1, valid1 = omega_solns_vec(q_sample, 1.0, k_in_sample_norm)
# etasign -1:
omega2, valid2 = omega_solns_vec(q_sample, -1.0, k_in_sample_norm)
omega = jnp.concatenate([omega1, omega2])
valid = jnp.concatenate([valid1, valid2])
q_sample = jnp.concatenate([q_sample, q_sample])
omega_valid = omega[valid]
q_sample_valid = q_sample[valid]
Into the lab frame#
With the omega angles determined, we can rotate q_sample into the lab frame:
[9]:
q_lab = sample_to_lab_vec(q_sample_valid, omega_valid, wedge, chi, dty, y0)
[10]:
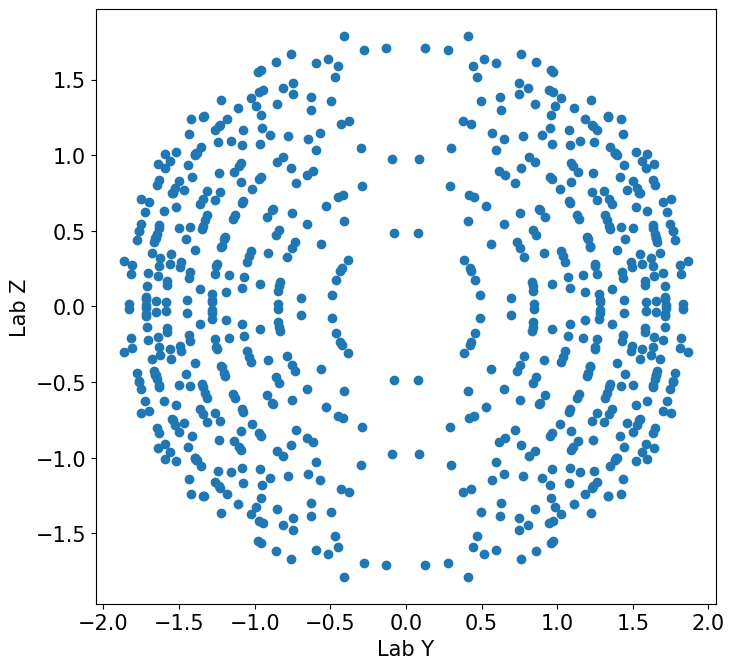
fig, ax = plt.subplots(figsize=(8,8))
ax.scatter(q_lab[:, 1], q_lab[:, 2])
ax.set_aspect(1)
ax.set(xlabel='Lab Y', ylabel='Lab Z')
plt.show()
Into the detector#
Now we can forward-project them into the detector!
Let’s set up the detector transforms:
[11]:
y_center = 1000.0
z_center = 1000.0
y_size = 75.0
z_size = 75.0
tilt_x = 0.0
tilt_y = 0.0
tilt_z = 0.0
distance = 180e3
o11 = 1
o12 = 0
o21 = 0
o22 = 1
det_trans, beam_cen_shift, x_distance_shift = anri.geom.detector_transforms(
y_center,
y_size,
tilt_y,
z_center,
z_size,
tilt_z,
tilt_x,
distance,
o11,
o12,
o21,
o22
)
We get the detector basis vectors in the lab frame:
[12]:
sc_lab, fc_lab, norm_lab = anri.geom.detector_basis_vectors_lab(det_trans, beam_cen_shift, x_distance_shift)
Now we can map into detector space:
[13]:
origin_lab = jnp.array([0., 0, 0])
# get outgoing scattering vector
k_out = q_lab_to_k_out_vec(q_lab, k_in_lab_norm)
# ray-trace it into the detector
sc, fc = raytrace_to_det_vec(k_out, origin_lab, sc_lab, fc_lab, norm_lab)
Results#
[14]:
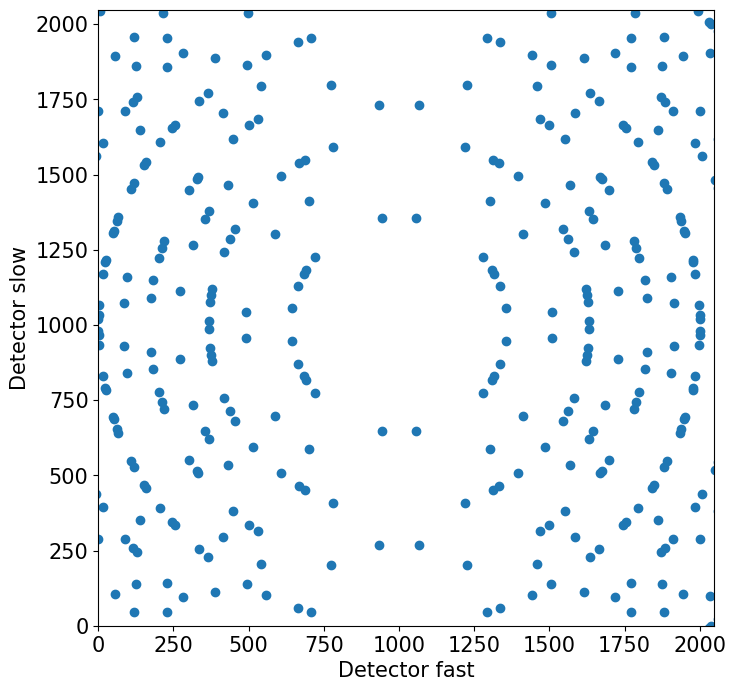
fig, ax = plt.subplots(figsize=(8,8))
ax.scatter(fc, sc)
ax.set_aspect(1)
ax.set(xlabel='Detector fast', ylabel='Detector slow')
# set some sensible detector limits
ax.set_xlim(0, 2048)
ax.set_ylim(0, 2048)
plt.show()
[15]:
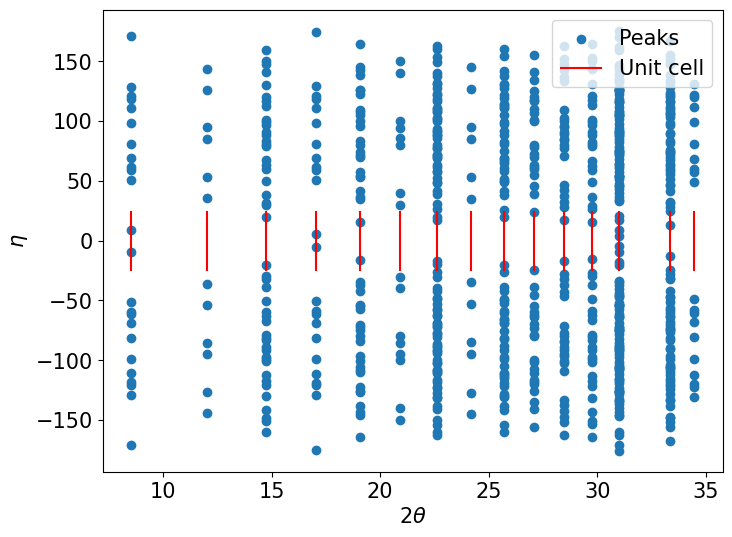
tth, eta = q_lab_to_tth_eta_vec(q_lab, wavelength)
[16]:
fig, ax = plt.subplots(figsize=(8,6))
ax.scatter(tth, eta, label='Peaks')
ax.vlines(struc.ringtth, -25, 25, color='red', label='Unit cell')
ax.set(xlabel=r'$2\theta$', ylabel=r'$\eta$')
ax.legend(loc='upper right')
plt.show()
Index the forward-simulated peaks with ImageD11#
As a sanity check, we should be able to index the peaks with ImageD11 and recover the UBI.
Let’s prepare the columnfile for ImageD11
[17]:
import ImageD11.columnfile, ImageD11.parameters, ImageD11.unitcell, ImageD11.indexing, ImageD11.grain
# make an ImageD11 unitcell from our structure
uc = ImageD11.unitcell.unitcell(struc.lattice_parameters, struc.sgno)
# prepare a minimal columnfile - just add detector positions and omega angles
cf_obs = ImageD11.columnfile.columnfile(new=True)
cf_obs.nrows = fc.shape[0]
cf_obs.addcolumn(fc, 'fc')
cf_obs.addcolumn(sc, 'sc')
cf_obs.addcolumn(omega_valid, 'omega')
# prepare parameters object to hold our experiment state
pars = ImageD11.parameters.parameters()
# detector
pars.set('distance', distance)
pars.set('tilt_x', tilt_x)
pars.set('tilt_y', tilt_y)
pars.set('tilt_z', tilt_z)
pars.set('y_size', y_size)
pars.set('z_size', z_size)
pars.set('y_center', y_center)
pars.set('z_center', z_center)
pars.set('o11', o11)
pars.set('o12', o12)
pars.set('o21', o21)
pars.set('o22', o22)
# beam
pars.set('wavelength', wavelength)
# diffractometer
pars.set('chi', chi)
pars.set('wedge', wedge)
pars.set('t_x', 0)
pars.set('t_y', 0)
pars.set('t_z', 0)
pars.set('omegasign', 1)
cf_obs.parameters = pars
print(pars.get_parameters())
{'distance': 180000.0, 'tilt_x': 0.0, 'tilt_y': 0.0, 'tilt_z': 0.0, 'y_size': 75.0, 'z_size': 75.0, 'y_center': 1000.0, 'z_center': 1000.0, 'o11': 1, 'o12': 0, 'o21': 0, 'o22': 1, 'wavelength': 0.3, 'chi': 0.0, 'wedge': 0.0, 't_x': 0, 't_y': 0, 't_z': 0, 'omegasign': 1}
Now we compute the peak geometry with ImageD11:
[18]:
print(cf_obs.titles)
cf_obs.updateGeometry()
print(cf_obs.titles)
['fc', 'sc', 'omega']
['fc', 'sc', 'omega', 'xl', 'yl', 'zl', 'tth', 'eta', 'ds', 'gx', 'gy', 'gz']
Sanity check - we should compute the same g-vectors in the sample frame (q_sample):
[19]:
jnp.abs(jnp.stack([cf_obs.gx, cf_obs.gy, cf_obs.gz], axis=1) - q_sample_valid).max()
[19]:
Array(1.72084569e-15, dtype=float64)
Now let’s set up our indexer and run it:
[20]:
ImageD11.indexing.loglevel = 3
idx = ImageD11.indexing.indexer_from_colfile_and_ucell(cf_obs, uc)
idx.ds_tol = 0.005
idx.assigntorings()
idx.hkl_tol = 0.01
idx.score_all_pairs()
[21]:
id11_ubi = idx.ubis[0]
id11_grain = ImageD11.grain.grain(id11_ubi)
# B matrices should be very similar:
print(jnp.abs(id11_grain.B - struc.B).max())
# the U matrices that we get back should be the same under symmetry:
dU = id11_grain.U.T @ U
print(dU)
2.3266697698128224e-16
[[ 1.01323425e-16 -1.00000000e+00 -4.57624723e-16]
[ 8.23611240e-16 -3.48230547e-16 1.00000000e+00]
[-1.00000000e+00 1.20547788e-17 6.47714064e-16]]
An even simpler check is whether our UBI from Anri indexes the g-vectors from ImageD11:
[22]:
from ImageD11.cImageD11 import score
gve_id11 = jnp.stack([cf_obs.gx, cf_obs.gy, cf_obs.gz], axis=1)
score_result = score(ubi=jnp.linalg.inv(U @ struc.B), gv=gve_id11, tol=0.01)
print(f'Score result: {score_result}, Peaks in dataset: {cf_obs.nrows}')
Score result: 736, Peaks in dataset: 736
created an array from object
created an array from object
[23]:
end = time.time()
print(f'Took {(end - start):.1f} seconds')
Took 4.5 seconds